√無料でダウンロード! おうぎ形の面積 988849-扇形の面積の求め方
この中心角 \(1°\)のおうぎ形が \(75\) 個集まると、その面積は 円の面積\(×\displaystyle \frac{1}{360}×75\) これがおうぎ形の公式の意味するところです。 おうぎ形の面積 もう1つの方法 おうぎ形の面積には、もう \(1\) つ覚えておいて損のない公式があります。・おうぎ形の面積の求め方を確認させる。 ・円の面積の求め方,それぞれのおうぎ形は円の 何分の何になるのかを確認させる。 (一斉指導) ・画用紙で作った図を提示しながら,どういう情 報があれば影の部分の面積が解けるのか問いか答え おうぎ形の面積が与えられているので こちらの公式を利用します。 まずは、半径9㎝の円の面積を求めます。 そして、公式にそれぞれの値をあてはめていくと 約分をしていきましょう。 (πも約分で消えてしまいます) (2)半径 ㎝、弧の長さ cmの
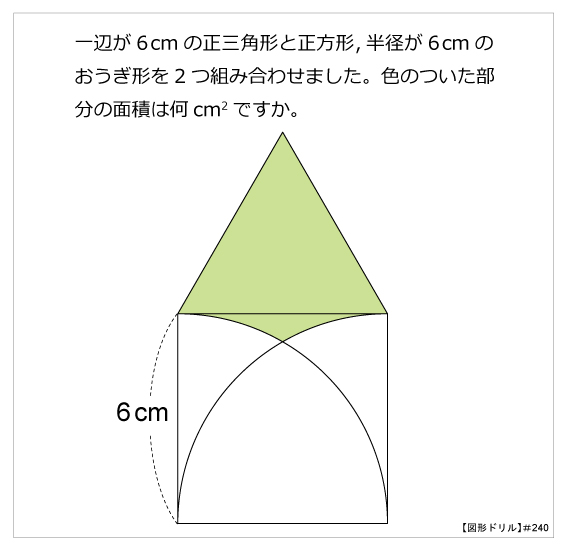
第240問 正方形と正三角形とおうぎ形 図形ドリル 第240問 正方形と正三角形とおうぎ形 算数星人のweb問題集 中学受験算数の問題に挑戦
扇形の面積の求め方
扇形の面積の求め方- 基本的なおうぎ形の面積の出し方 与えられている長さが「対角線」ではなく「直径や半径」なら簡単ですね? 円を4等分した形に見えますので、まずは分割する前の状態に戻してみます。 まずはこの図から「円」の面積を求めてみます。 木の葉形の面積(1997 灘中 改題) 木の葉形面積(灘中1998 類題) 平面図形の面積(灘 07) 正三角形と正六角形 平面図形の面積 (三田学園 1998 改題) 半円とおうぎ形の面積(SAPIX算数補充プリント) 正三角形と半円(灘中学 受験算数問題より) 木の



3分で分かる 扇形 おうぎ形 の面積と弧の長さの求め方 公式をわかりやすく 合格サプリ
円とおうぎ形のいろいろな面積の問題です。 学習のポイント 正方形とおうぎ形を合わせた形の面積を素早く求められるようにしましょう。 *色のついた部分の面積を求めます。 4分の1のおうぎ形2つから正方形をひく、4分の1のおう右の図は円 錐 すい の展開図であり,側面のおうぎ形の中心角は1°で,底面の円の半径は4㎝である。 このとき,側面のおうぎ形の半径を求めなさい。円錐の表面積を求める公式は、S = πr(rR) で表されます ♦ このページでは、「公式を使う場合」と「使わない場合」に分け、円錐の表面積の求め方を例題と共に説明しています。
なので、これを面積を求める式に代入してみます。 これで中心角が分からなくても母線 x と弧の長さ z さえわかればおうぎ形の面積を求められます。 あとはこの式を整理すると、、、 よって、おうぎ形の面積は 「母線の長さ × 弧の長さ ÷ 2」 で求める そして、おうぎ形の面積の公式は よって、底面のおうぎ形の面積は2/3cm2 (6π×1/9 =2π/3) また、底面は2つあるので、2倍して、4π/3cm2。 次に側面積です。 正面と、その左側の面積は同じです。 「底辺×高さ」で、15cm2(3×5) また、それが二つなので、30cm2。おうぎ形は円の一部であることを理解させる。 3 おうぎ形の弧や面積は、同一円の中心角の大きさに比例していることを理解させる。 4 おうぎ形の弧や面積を自ら計算し、求めることができるようにさせる。 • 時間配当 1
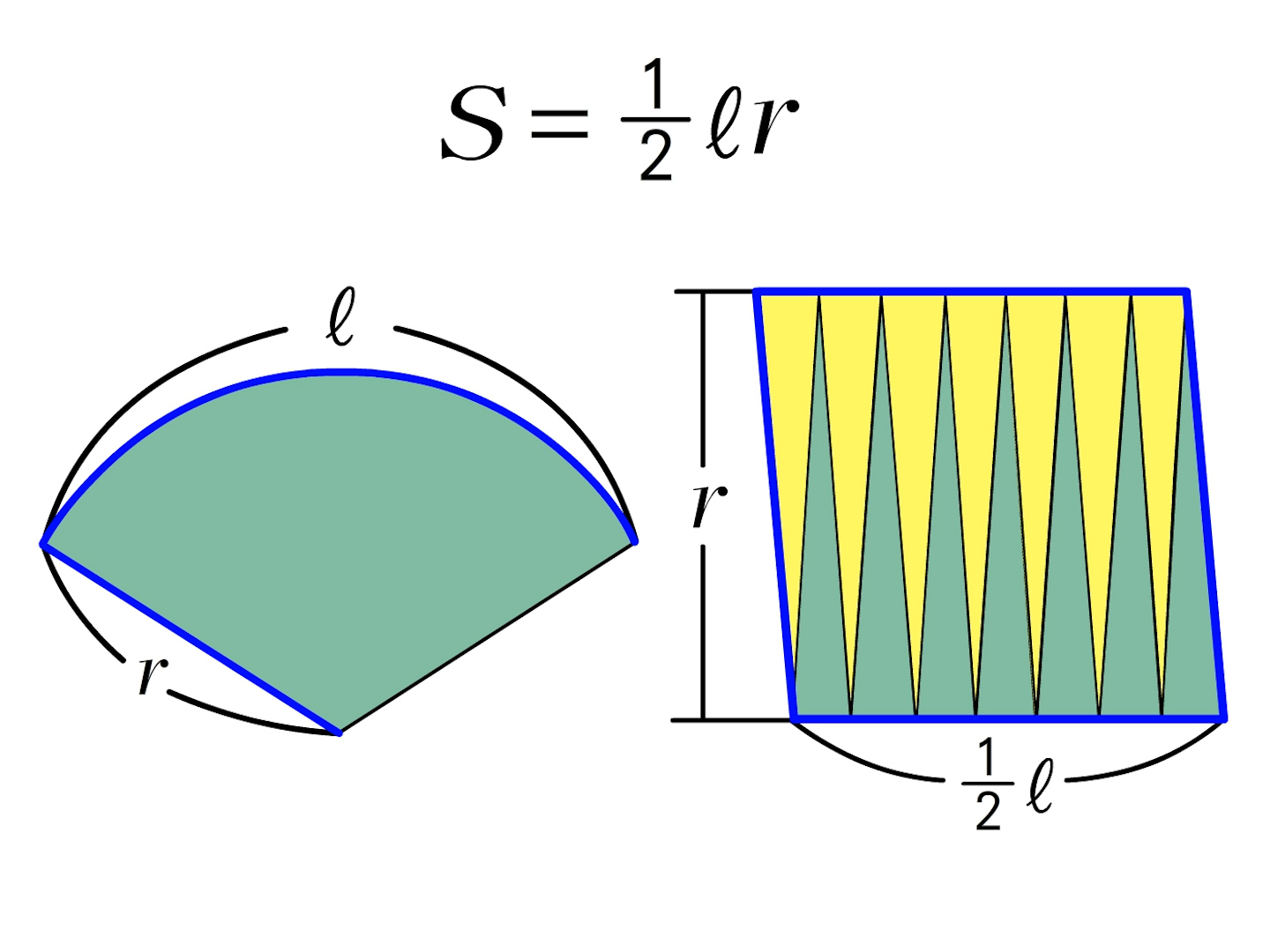
扇形の面積を求める公式は、S = πr^2 × x/360 = 1/2 lr で表されます。このページでは、扇形の面積の求め方を、計算問題と共に説明しています。また、公式の導き方も説明しています。よって、おうぎ形の面積と弧の長さは以下のように求めることができます。 お う ぎ 形 の 面 積 中 心 角 お う ぎ 形 の 弧 の 長 さ 中 心 角 お う ぎ 形 の 面 積 π r 2 × 中 心 角 360 ° お う ぎ 形 の 弧 の 長 さ 2 π r × 中 心 角 360おうぎ形の面積を考えてみます。 弧の長さが l l ,半径が r r のおうぎ形を細かく切ると平行四辺形のようになります。 おうぎ形の面積は,底辺が 1 2l 1 2 l ,高さ r r の平行四辺形の面積と同じになります。 実施時期 1年生2学期(11月) 単元項目 5章1節
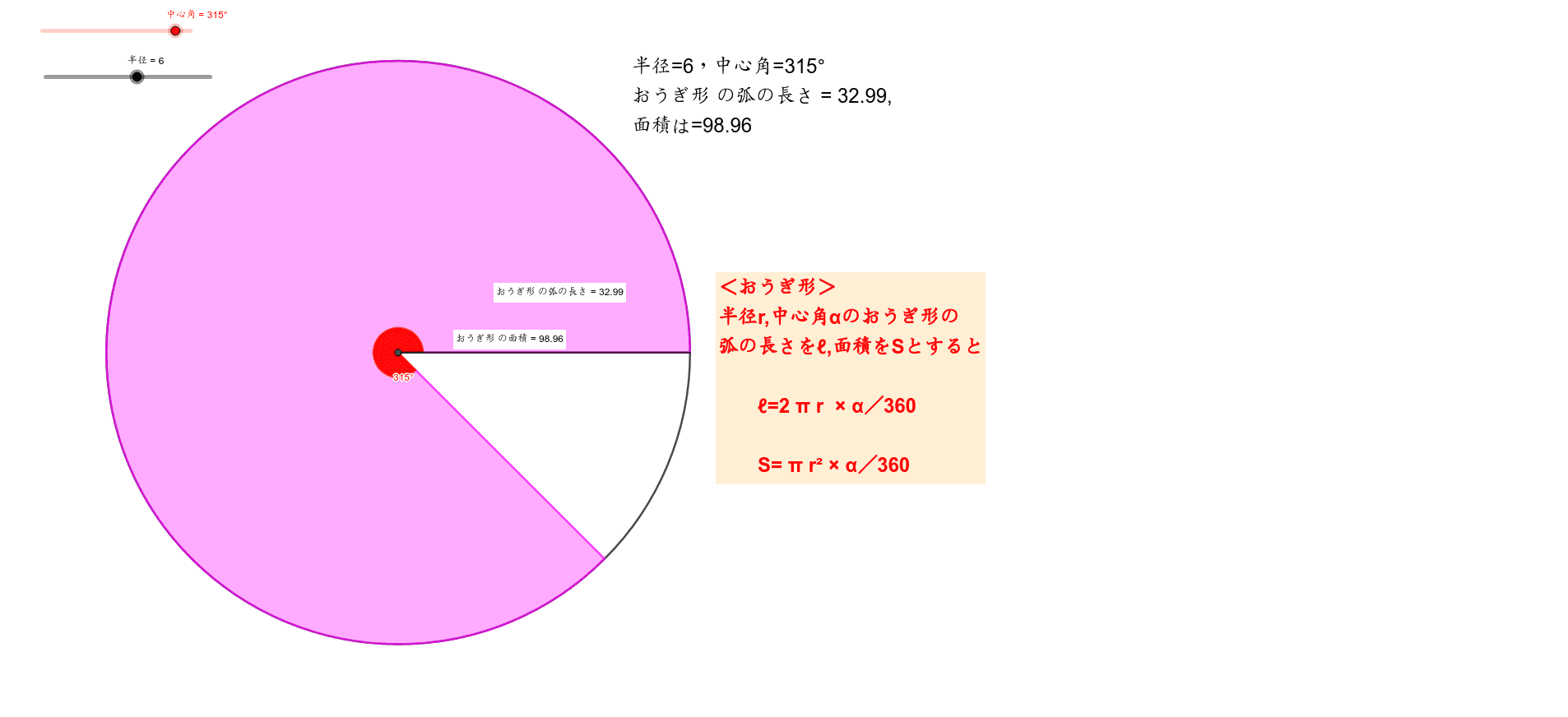



中1 おうぎ形の弧の長さや面積について考えよう Geogebra



高校入試数学 おうぎ形についての公式まとめとその練習問題
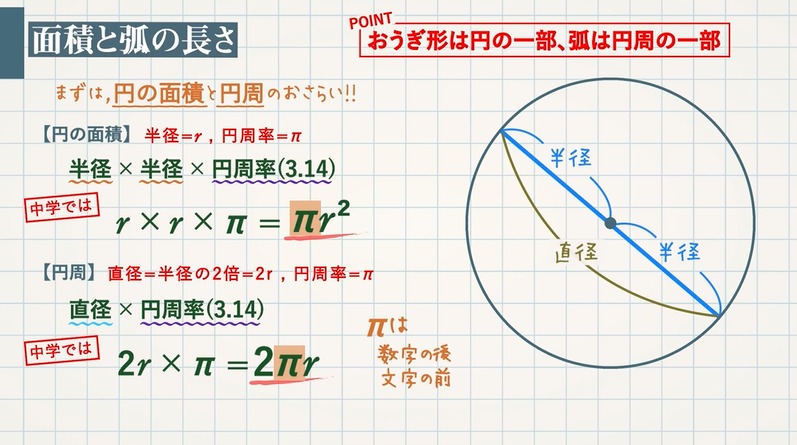
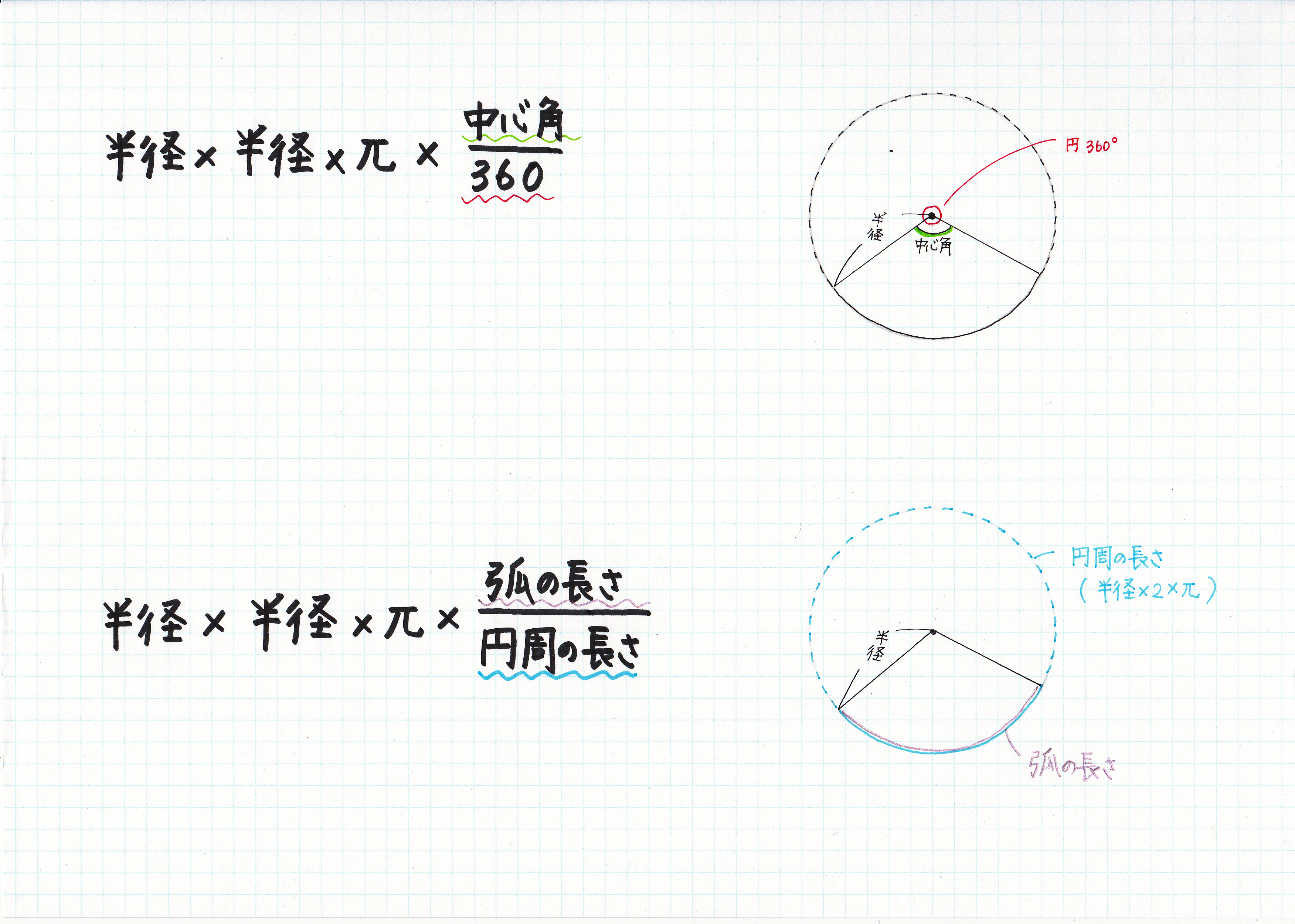
おうぎ形の弧の長さや面積は中心角に比例するので, おうぎ形の弧の長さや,面積を求めるには, 円周の長さや,円の面積に 中心角 360° をかければよい。 半径rで中心角がaのおうぎ形 弧の長さ l = 2πr × a 360 面積 S = πr2 × a 360 例半径18cm, 中心角40°の おうぎ形の半径は、正方形の一辺の長さと等しく、 6cm 6 c m です。 また、中心角は、正方形の1つの角と等しいので、 90∘ 90 ∘ です。 以上から、面積は 62 −62 ×π × 90 360 = 36 −9π 6 2 − 6 2 × π × 90 360 = 36 − 9 π なので、 (36−9π)cm2 ( 36 − 9 π) c m 2 となり 円の面積のまとめ ・円の面積=半径×半径×314 ・おうぎ形の 面積=半径×半径×314× 中 心 角 中 心 角 360 ° 弧の長さ=円周× 中 心 角 中 心 角 360 ° かずのかず 以上、「算数嫌いな人が、 算数を楽しく好きになって欲しい」 かずのかずでした




扇形の公式は暗記しない 割合という考え方を導入するだけでスラスラ解ける 中学受験ナビ
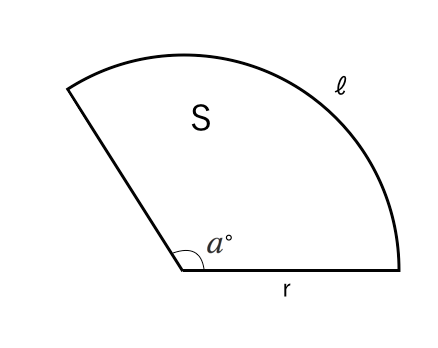



おうぎ形の問題 ちょっと応用編 苦手な数学を簡単に
ひし形の面積=対角線×対角線÷2 台形の面積= (上底+下底)×高さ÷2 三角形の面積=底辺×高さ÷2 円の面積=半径×半径×円周率 (314) おうぎ形の面積=半径×半径×円周率×中心角/360° 公式の成り立ちから知りたい人や公式がまだ曖昧な人は、下記の平面おうぎ形の公式 弧の長さ = 円周 × 中心角 360° 中 心 角 360 ° = 直径×314 × 中心角 360° 中 心 角 360 ° おうぎ形の面積 = 円の面積 × 中心角 360° 中 心 角 360 ° = 半径×半径×314 × 中心角 360° 中 心 角 360 ° 重要なのは、 おうぎ形が元の円と比べた時に 扇形(おうぎ形)の面積の求め方 扇形の面積を求めるときには次の公式を使います。 扇形の面積 =半径×半径×円周率× ※扇形の面積は、円の面積に をかけることで求めることが出来ます。 ※円周率は、小学校ではふつう314を使います。




円とおうぎ形 応用 無料で使える中学学習プリント




中1 数学 中1 75 おうぎ形の弧と面積 基本編 Youtube
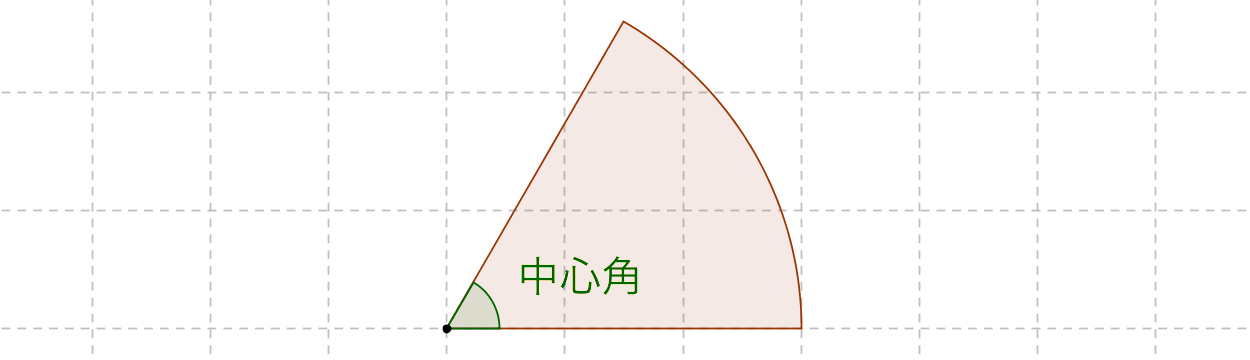
円の面積の式 $$\Large{π}r^2$$ 円の円周の式 $$\Large{2}{π}{r}$$ 次に下の図のように、この円を一部を切っておうぎ形を作ったとき、 おうぎ形の面積は、円の全体の面積の割合になっているでしょうか? ここで、おうぎ形が元の円の何割か? 求めるおうぎ形の面積は このおうぎ形の面積は、 元の円の面積の 6分の1 であるから $3\times3\times314\times\frac{\displaystyle 1}{\displaystyle 6}=\underline{471 cm^2 \dots Ans}$ おうぎ型・スーパー三角形の公式 おうぎ形の面積 基本円とおうぎ形 では、おうぎ形の弧の長さを求めるときに、円周を分割して求めました。 中心角が 60∘ 60 ∘ だったら、1周 360∘ 360 ∘ に対する割合を考えればいいのでした。 おうぎ形の面積も同様に考えます。 上の図は、半径 12



1年 おうぎ形の面積 数学イメージ動画集 大日本図書
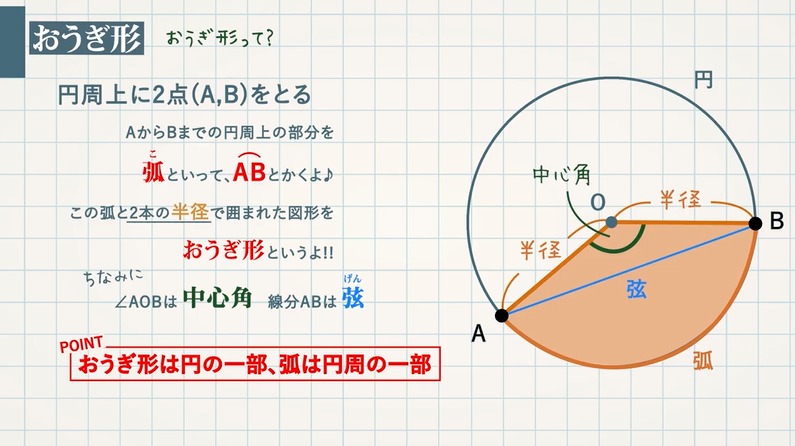



おうぎ形まとめ 弧と面積の求め方 教遊者
おうぎ形の面積(等積移動系)を求めよ問題のパターン 1 等積移動:同じ面積の所に移動させて計算しやすくする 2 葉っぱ4枚:小さい正方形4つに分ける(正方形の面積×057) 3 補助線+等積移動:補助線を引いて等積移動する 4 ヒポクラテスの三日月 これもおうぎ形が 円の面積のどのくらいを占めているのか を表しています。 例えば中心角が\(90^{\circ}\)のおうぎ形の面積を求めてみます。 図のように中心角が\(90^{\circ}\)のおうぎ形は元の円の\(\frac{1}{4}\)です。半径16cmで中心角315°のおうぎ形の弧の長さを求めよ。 半径12cmで中心角80°のおうぎ形の面積を求めよ。 半径10cmで中心角°のおうぎ形の面積を求めよ。 半径 9 2 cmで中心角160°のおうぎ形の面積を求めよ。 半径3㎝、中心角1°のおうぎ形がある。 弧の長さを




扇形の面積の出し方と特殊な場合の公式 たぬぬ塾 中学校の先生たち




標準 おうぎ形の弧の長さや面積 なかけんの数学ノート
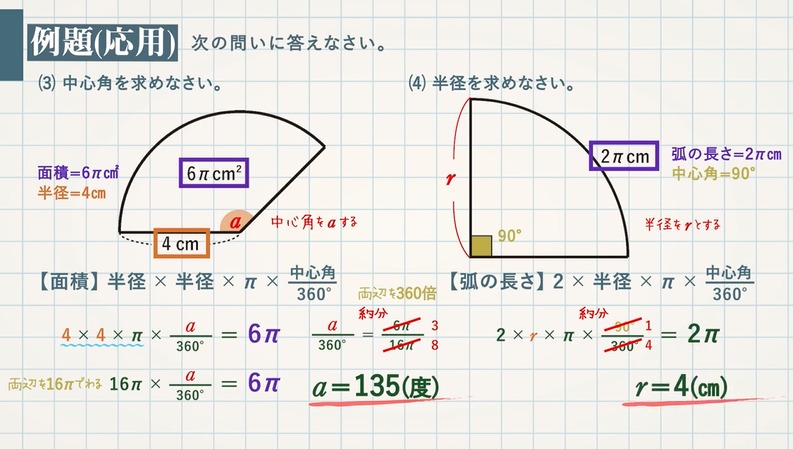
例題 半径5cmの半円を、円Aを中心にして、45°回転させました。 黒くぬった部分の面積を求めなさい。おうぎ形の面積 を 求める力 が、理解できていれば、小学生が自分の力で、解答を導けるプリントを作りました♪パパママ向けのヒント解説も行っていますよ♪おうぎ形について、以下の問いに答えなさい。 1 半径12cm、中心角25°のおうぎ形の面積と孤の長さを求めなさい。 2 半径16cm、孤の長さが12πcmのおうぎ形の中心角を求めなさい。図をもとに式を立てよう! おうぎ形については、 中心角が90° だから、 (おうぎ形1つの面積)=3×3×π×90/360 (三角形の面積)=3×3×1/2 これらを利用すれば、求める ラグビーボールの面積 が求められるね。 練習の答え



よく出題される おうぎ形の部分面積 暁星中学 2012年 改題 これが中学入試に出た図形問題




扇形の面積 弧の長さ まわりの長さの求め方 公式 小学生 中学生の勉強
おうぎ形の弧の長さと面積は下のプリントのように求めます。半径をr、中心角をa°とします。 弧の長さ 面積 重要なポイントは下の動画で解説しています。弧の長さも面積も、もともとの円の円周や面積にa°/360°をかけて求めます。



おうぎ形まとめ 弧と面積の求め方 教遊者




円 扇形 の面積 周や弧の長さの公式 数学fun




数学パズル 意外と悩むおうぎ形の面積問題 ひらめいたらスッキリします Youtube




中学数学 3分で簡単にわかる 扇形 おうぎ形 の面積の求め方 の公式 Qikeru 学びを楽しくわかりやすく



扇形とは 面積 中心角 半径 弧の長さの公式と求め方 受験辞典




3分で分かる 扇形 おうぎ形 の面積と弧の長さの求め方 公式をわかりやすく 合格サプリ



1



円とおうぎ形 いろいろな面積の問題 中学受験準備のための学習ドリル




第240問 正方形と正三角形とおうぎ形 図形ドリル 第240問 正方形と正三角形とおうぎ形 算数星人のweb問題集 中学受験算数の問題に挑戦




おうぎ形面積の超簡単な求め方 合同会社エスキージャパン




扇形の面積の求め方 小学生でも公式を簡単に使える問題です 中学や高校の数学の計算問題




おうぎ形 の弧の長さと面積 計算ドリル 問題集 数学fun




裏技 おうぎ形の面積を一瞬で求める 弧の長さを利用した裏技公式 中学数学 平面図形 2 Youtube




標準 おうぎ形と正方形の面積 なかけんの数学ノート




扇形の面積の求め方 公式と計算例




弧の長さを使った扇 おうぎ 型の面積の公式を知っていますか




中1 数学 中1 78 おうぎ形の弧と面積 さらにややこしい図形編 Youtube




おうぎ形の弧長 面積 中心角 半径 具体例で学ぶ数学




中1数学 おうぎ形の面積 弧の長さ 中心角の求め方がサクッとわかる 映像授業のtry It トライイット




おうぎ形の面積 弧度法との関連から眺める 身勝手な主張
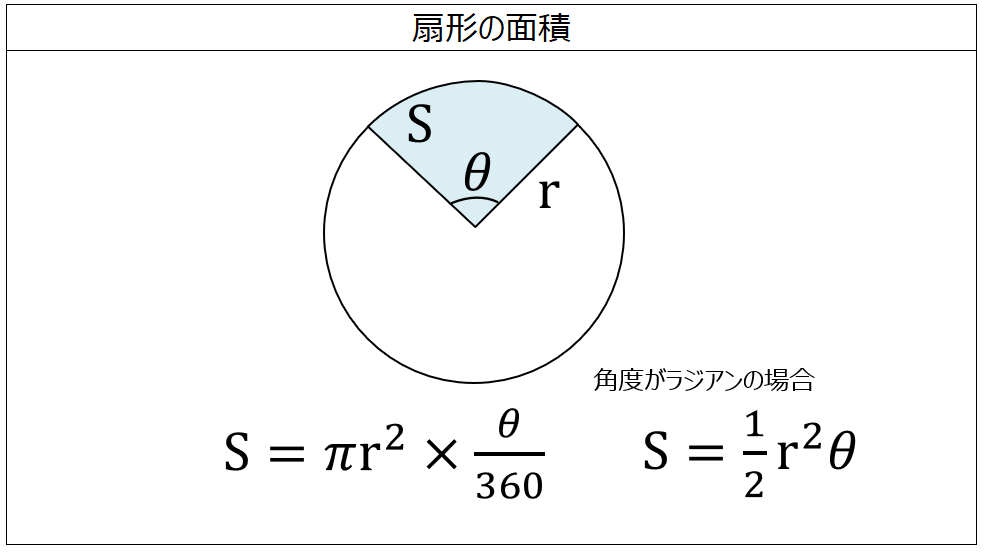



扇形の面積 製品設計知識



1
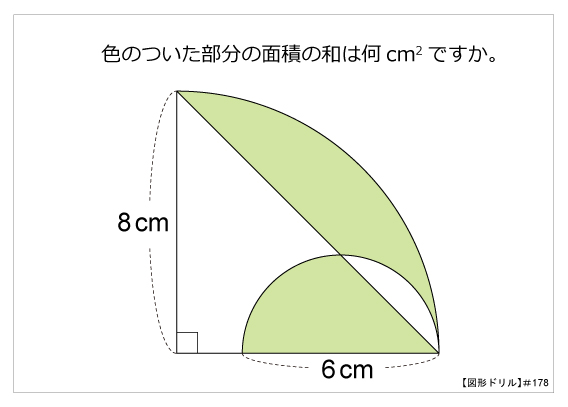



第178問 おうぎ形の複合図形 図形ドリル 第178問 おうぎ形の複合図形 算数星人のweb問題集 中学受験算数の問題に挑戦
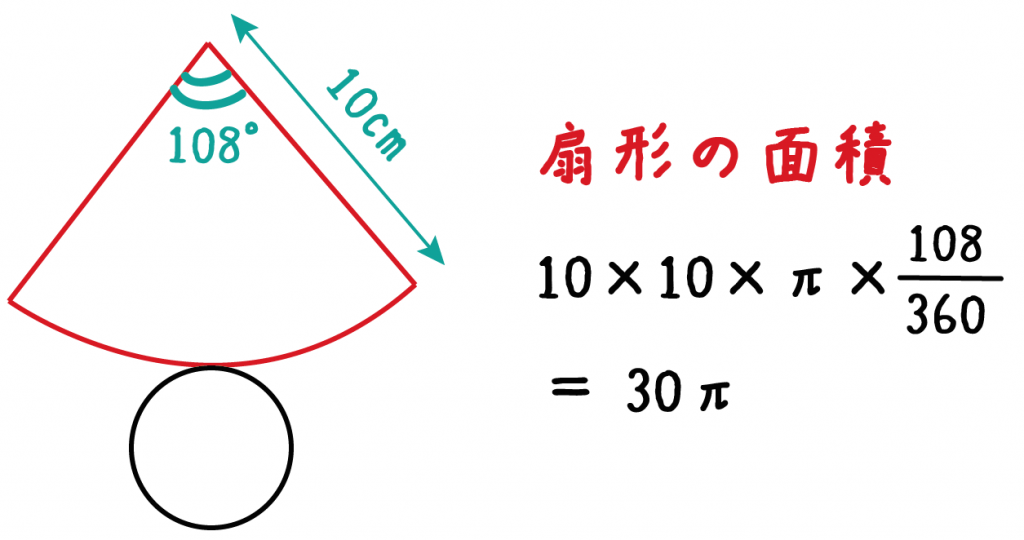



簡単公式 円錐の側面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




おうぎ形の面積 弧の長さ 数学ノート



三角形と扇形の面積 数学 化学講師 佐藤学による受験生に役立つ濃縮ポイントと Etc




扇形の面積公式が一目でわかる 丁寧な証明付き 高校生向け受験応援メディア 受験のミカタ



円とおうぎ形 中学受験 田中貴 Com




中学数学 3分で簡単にわかる 扇形 おうぎ形 の面積の求め方 の公式 Qikeru 学びを楽しくわかりやすく




おうぎ形 面積 弧の長さ 中心角の求め方を問題解説 数スタ




おうぎ形の弧と面積 Youtube
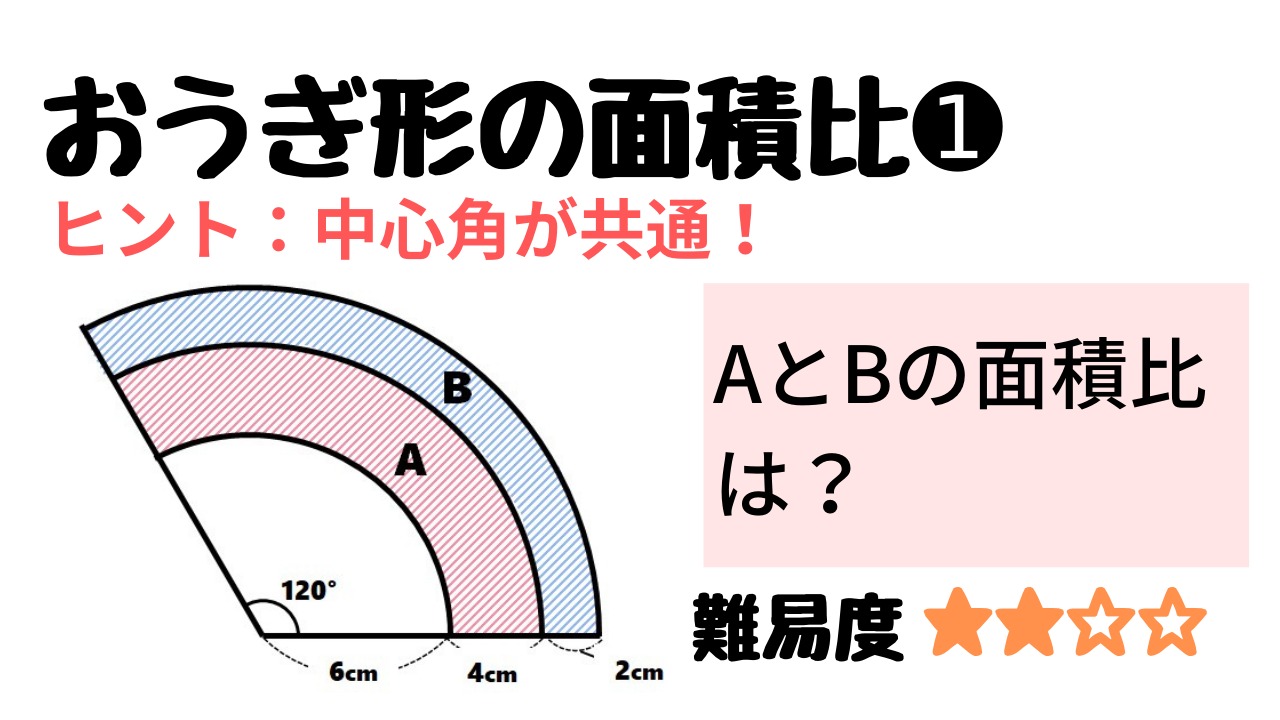



中学受験算数 中心角が等しいおうぎ形の面積比の問題 Stupedia




応用 おうぎ形と正方形の面積 なかけんの数学ノート




中1 数学 おうぎ形 これで基礎バッチリ 中学生 数学のノート Clearnote




中学数学 円とおうぎ形 中学数学の無料オンライン学習サイトchu Su




円 おうぎ形 の面積 Geogebra




おうぎ形の弧の長さ 面積 中心角の求め方と公式 Irohabook




中1 数学 中1 74 おうぎ形の弧と面積 Youtube



中1数学 円とおうぎ形 では 円の性質とおうぎ形の面積の求め方が項目理解の重要ポイント 桜華塾 お役立ちブログ 楽天ブログ
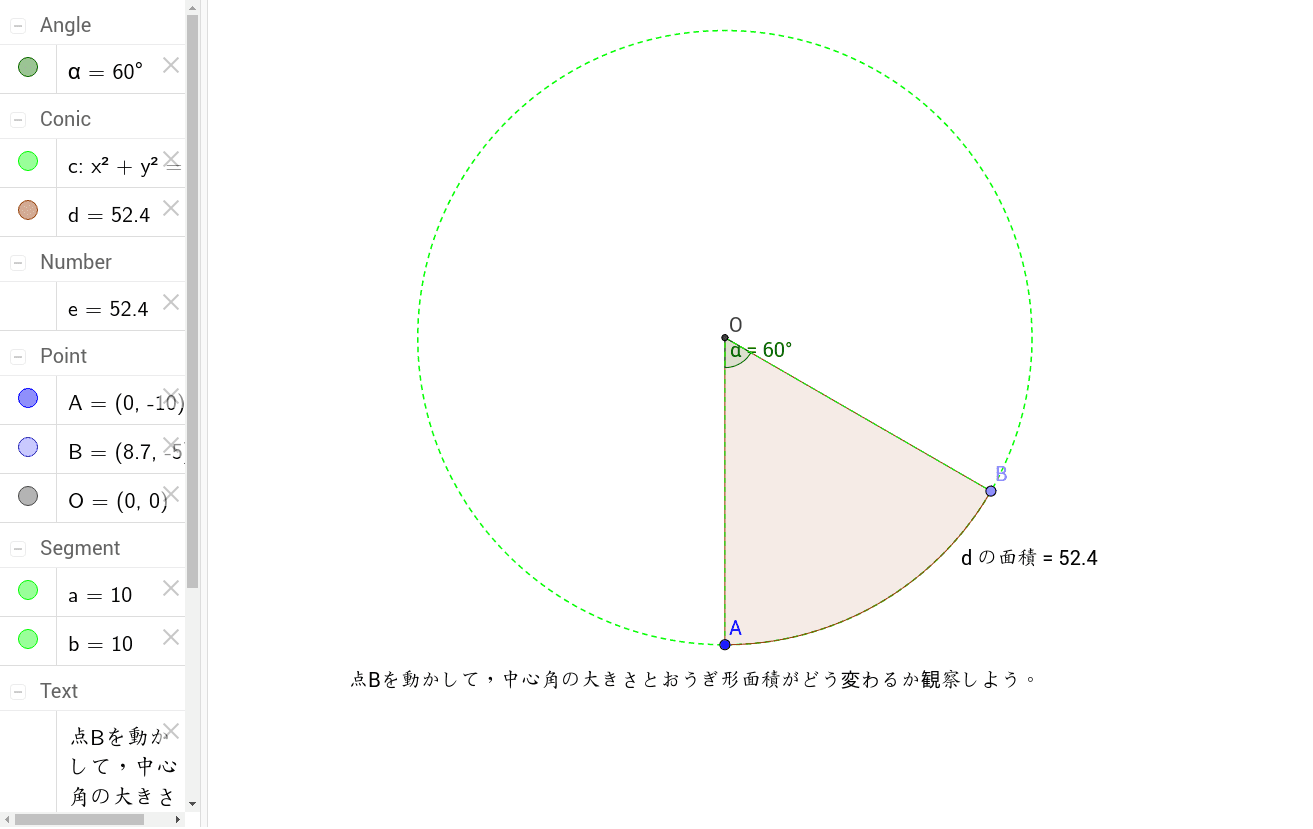



中心角とおうぎ形 Geogebra




なぜ おうぎ形の面積は1 2 弧の長さ 半径 なのか を説明します おかわりドリル
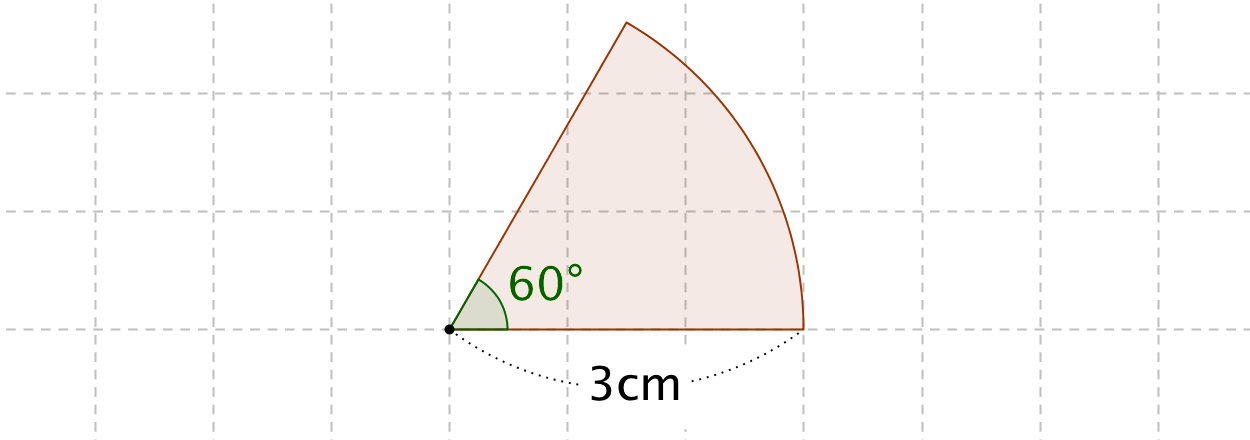



おうぎ形の面積の公式 算数の公式




扇形の弧の長さと面積 小学 中学数学での平面図形の求め方 リョースケ大学




中1数学 おうぎ形の面積 弧の長さ 中心角の求め方がサクッとわかる 映像授業のtry It トライイット



中学入試の図形の問題です 正方形とおうぎ形を組み合わせた以下の図形で Yahoo 知恵袋
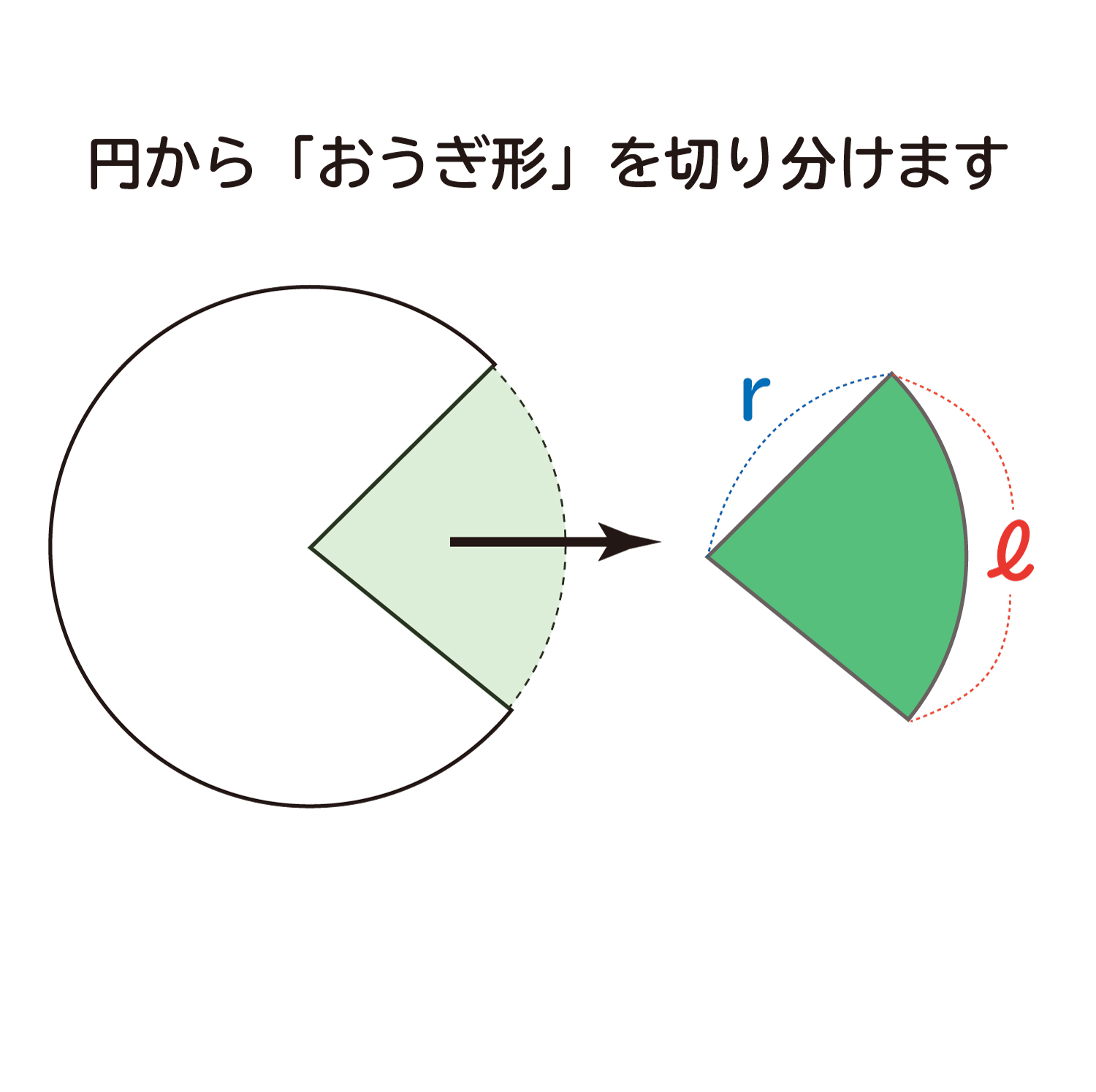



なぜ おうぎ形の面積は1 2 弧の長さ 半径 なのか を説明します おかわりドリル




半径6cm 弧の長さ2pcmのおうぎがたの面積 はどーやって求めますか Clearnote




おうぎ形まとめ 弧と面積の求め方 教遊者
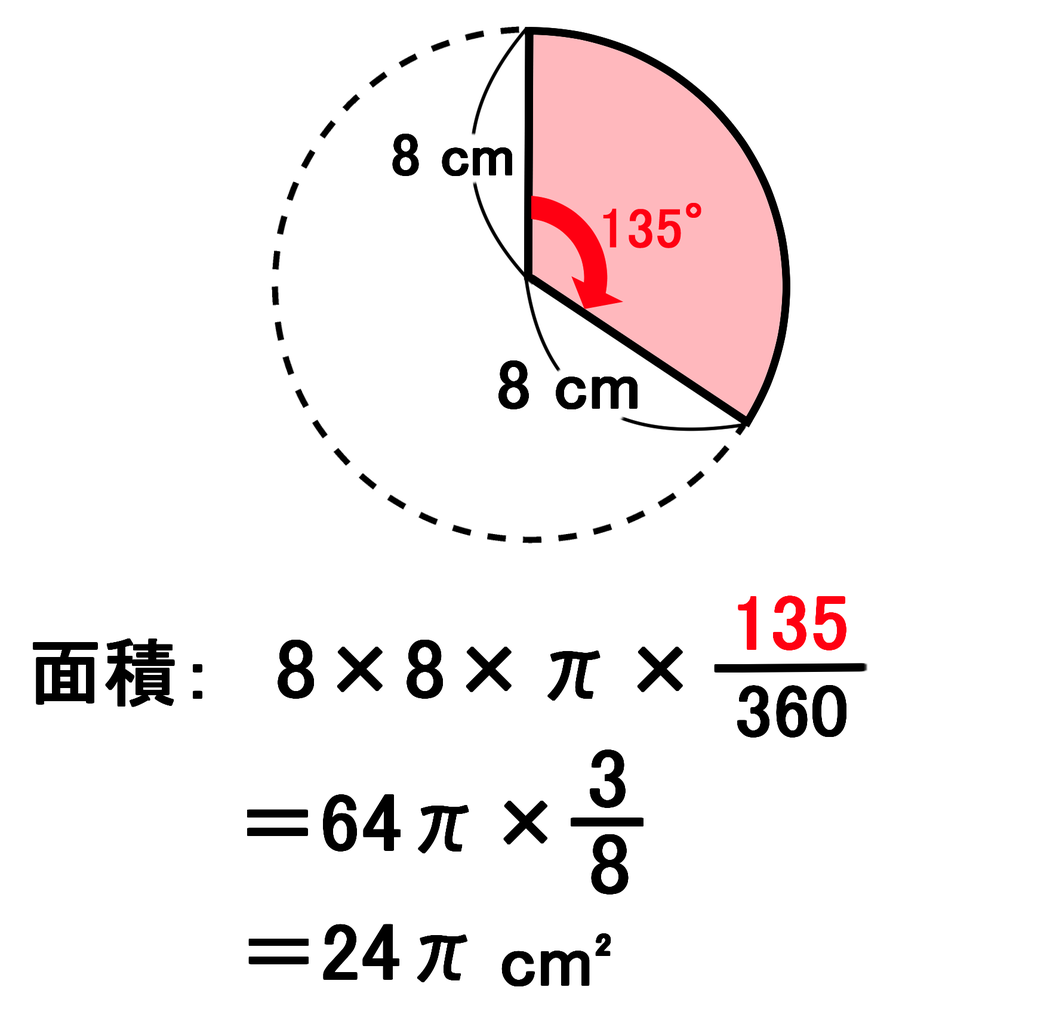



おうぎ形の面積と弧の長さの求め方 バカでもわかる 中学数学




中学数学 3分で簡単にわかる 扇形 おうぎ形 の面積の求め方 の公式 Qikeru 学びを楽しくわかりやすく




中1数学 おうぎ形の面積 弧の長さ 中心角の求め方がサクッとわかる 映像授業のtry It トライイット




おうぎ形の問題 ちょっと応用編 切り取って求める 苦手な数学を簡単に




扇形面積求め方 扇形の弧の長さと面積 小學 中學數學での平面図形の Txfs Co




正方形と扇形の面積をつかった問題がわかる3ステップ Qikeru 学びを楽しくわかりやすく
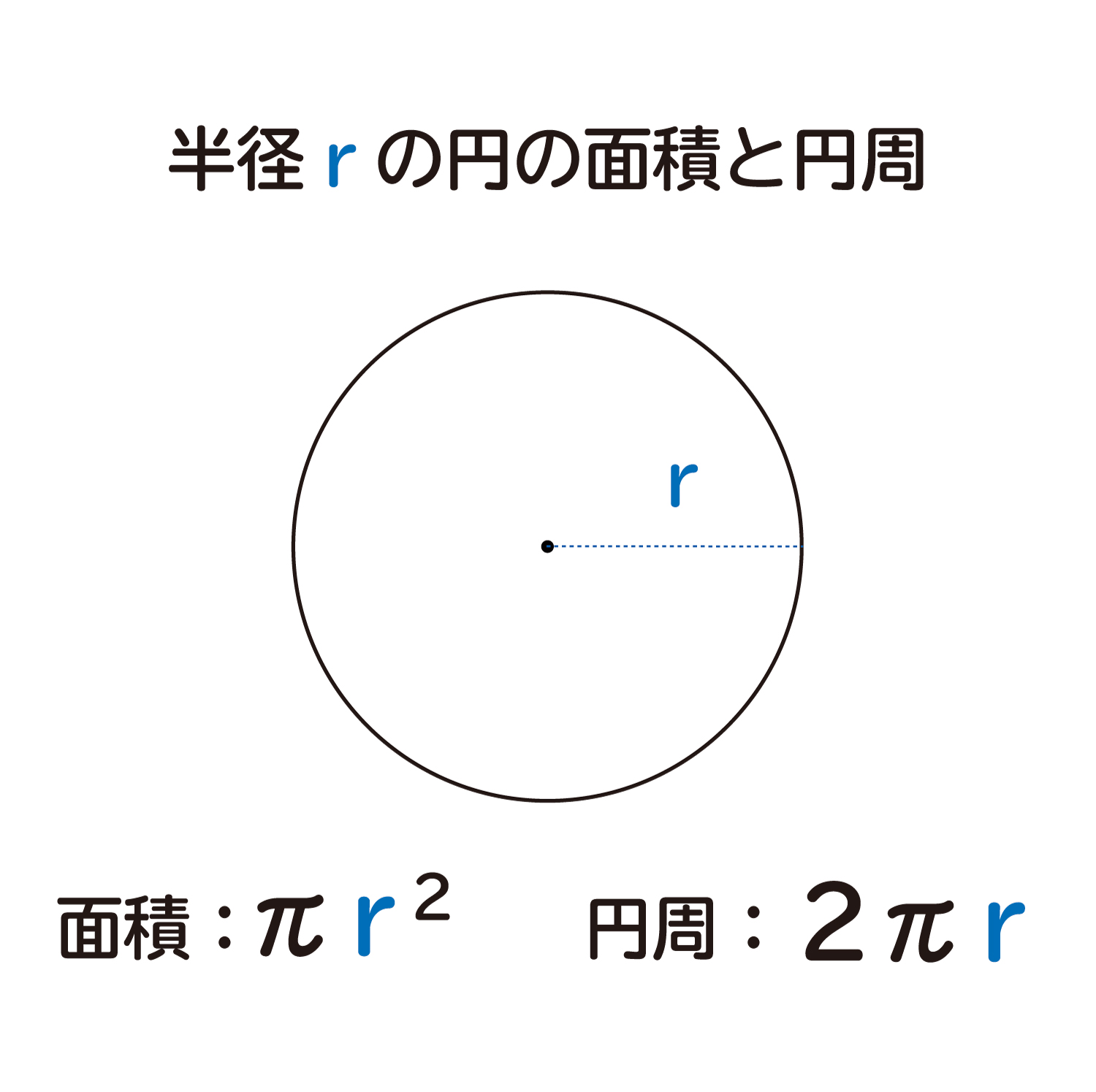



なぜ おうぎ形の面積は1 2 弧の長さ 半径 なのか を説明します おかわりドリル




おうぎ形まとめ 弧と面積の求め方 教遊者




中1数学 おうぎ形の面積 弧の長さ 中心角の求め方がサクッとわかる 映像授業のtry It トライイット




半円を回転させる面積の問題 プリントを使って自分で解こう
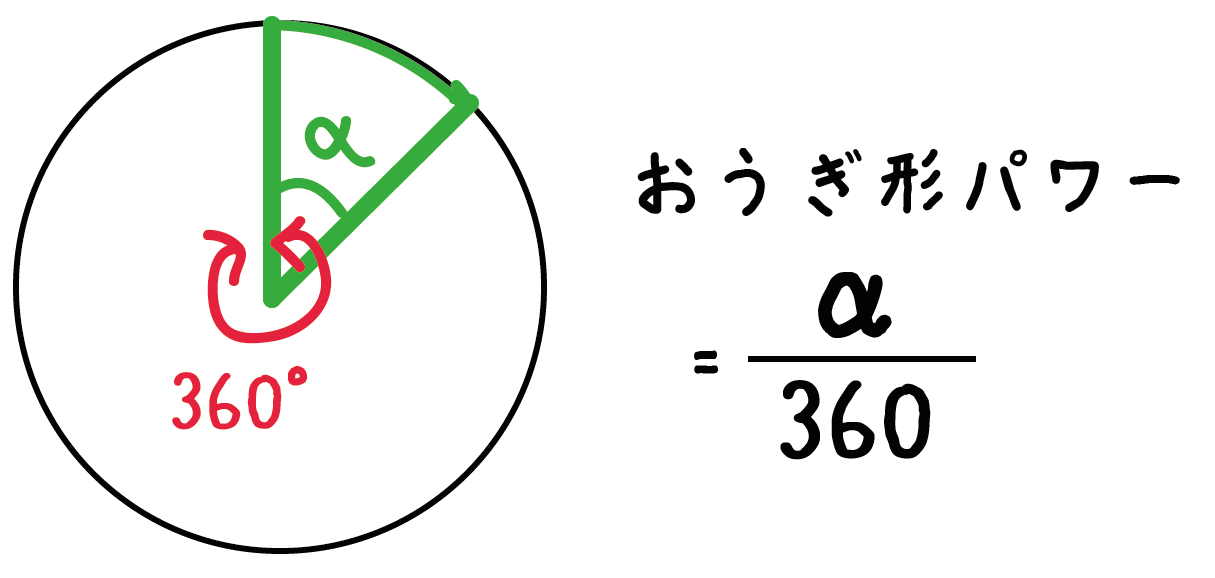



中学数学 3分で簡単にわかる 扇形 おうぎ形 の面積の求め方 の公式 Qikeru 学びを楽しくわかりやすく




中1数学 おうぎ形の応用問題 練習編 映像授業のtry It トライイット




中1数学のおうぎ形の公式が覚えられません そろそろテストなのでやばいんです Clearnote
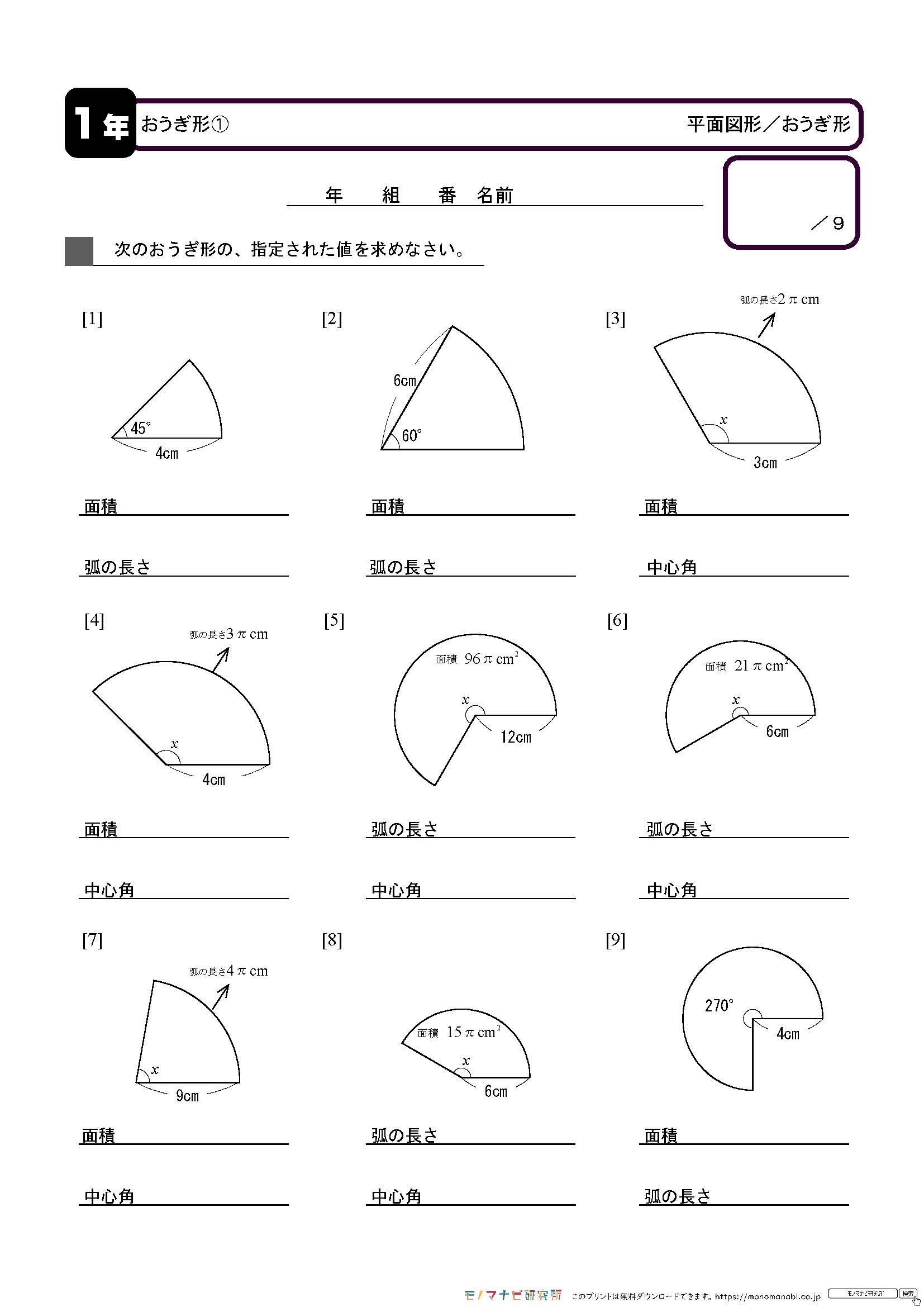



モノマナビ研究所
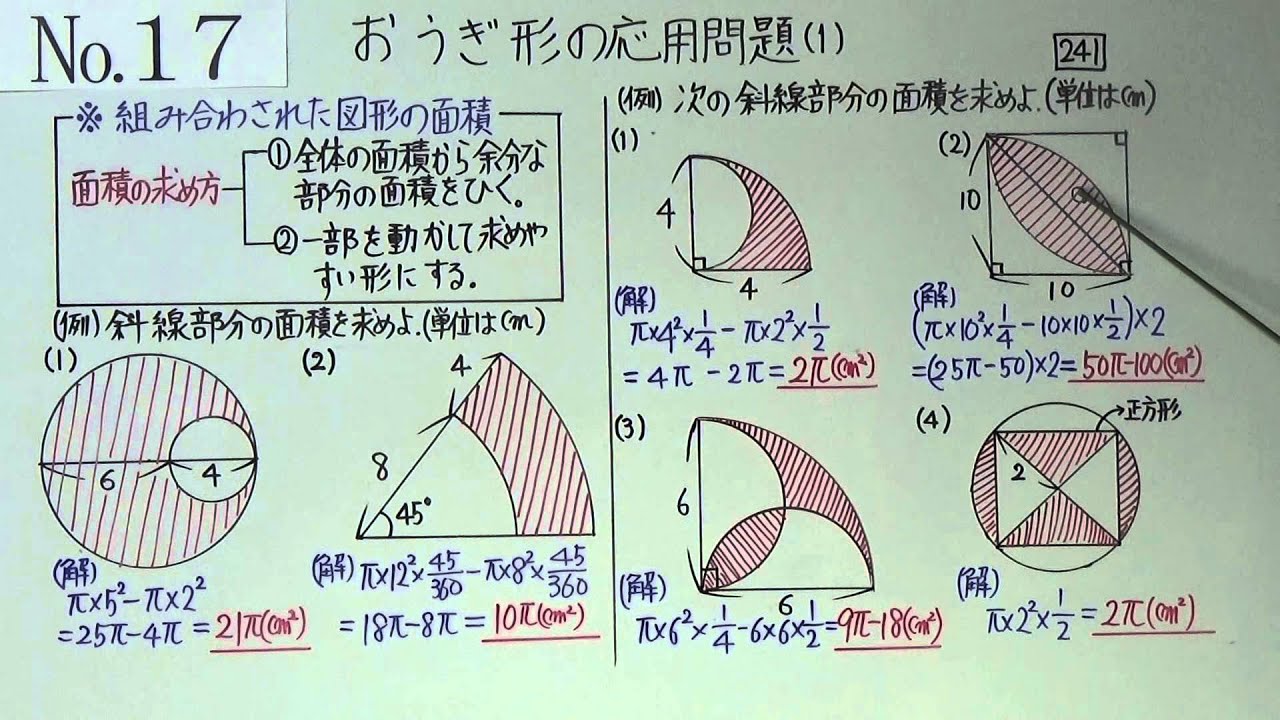



中1 17 2 おうぎ形の応用 1 Youtube




高校数学 一般角と弧度法 扇形の弧長l R8と面積s 1 2r 8 受験の月




扇 おうぎ 形の面積を求める公式と弧の長さの求め方




中学数学 3分で簡単にわかる 扇形 おうぎ形 の面積の求め方 の公式 Qikeru 学びを楽しくわかりやすく




なぜ扇形の面積にするという考えになるのですか 解説を見ても分かりませんでした Clearnote




カンタン公式 扇形の中心角の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




おうぎ形の弧の長さと面積の求め方 小学生に教えるための解説 数学fun




教えて下さい お願いします Clearnote




おうぎ形 半径の求め方は 問題を使って徹底解説 数スタ
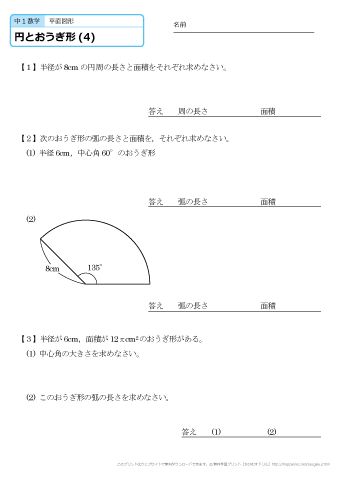



中学1年生 数学 円とおうぎ形 練習プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




中学1年生 数学 円とおうぎ形 練習プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




3分で分かる 扇形 おうぎ形 の面積と弧の長さの求め方 公式をわかりやすく 合格サプリ



おうぎ形の面積の公式 算数の公式




おうぎ形の面積と弧の長さの公式 全国 中学数学ができるようになるブログ




公式が覚えられない を解消 円とおうぎ形の周りの長さ 面積の求め方 中学受験ナビ
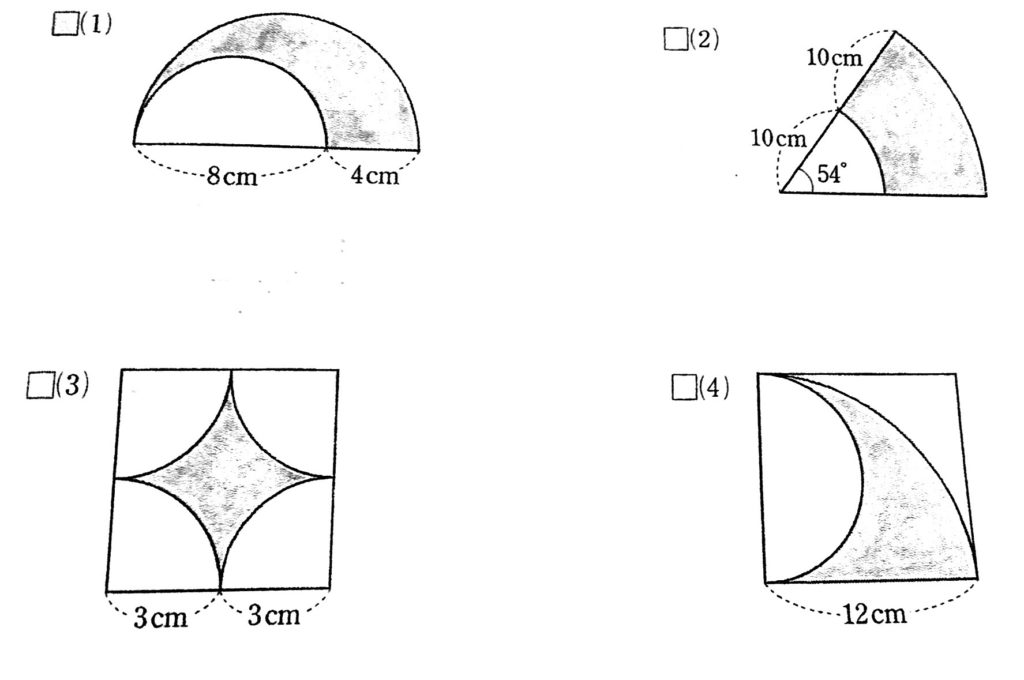



おうぎ形の応用 影の部分の面積 周の長さの求め方 数スタ




算数 本当に 分かる という事 おうぎ形の面積その1 エース学院
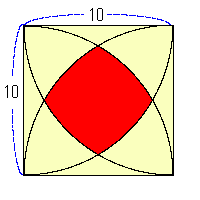



算数かと思ったら数学でした Npo Selfish セルフィッシュ




平面図形 おうぎ形の中心角の求め方 中学数学 定期テスト対策サイト



等しい面積を利用して解く頻出問題 算数解法の極意



おうぎ形まとめ 弧と面積の求め方 教遊者



1




おうぎ形の面積と弧の長さ Geogebra



おうぎ形の面積の公式について 現役塾講師のわかりやすい中学数学の解き方



みんなの算数オンライン 中学受験 4年 円とおうぎ形 円と面積応用 トレーニング
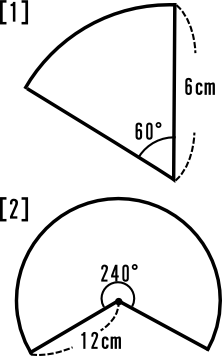



中学1年数学練習問題 円とおうぎ形の面積 円周 孤の長さ 空間図形




平面図形 おうぎ形の中心角 中学数学 定期テスト対策サイト



1
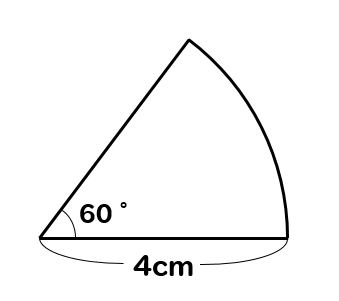



おうぎ形 注意 周りの長さを求める公式を解説 数スタ




円とおうぎ形 応用 無料で使える中学学習プリント
コメント
コメントを投稿